A fuzzy logika - alapismeretek

Ha valaki korábbi és mostani fuzzy logikával foglalkozó cikkeinket olvassa, joggal gondolhatja, hogy ez a dolog messzebb van az autófenntartás hétköznapjaitól, mint Makó lovag Jeruzsálemtől. Az éremnek itt is kettő vagy még több oldala van. Autóink „agyasak” és ma már programjuk sem kizárólag „huzalozott”, döntési logikájuknak – a feladatok rendkívüli bonyolultsága miatt – rendkívül gyorsnak, ezzel együtt a lehető legjobb közelítésűnek kell lennie. A fuzzy logika ebben segít. E lapszámunkban írt ZF CDC „Skyhook” rendszer is fuzzy logikára épít, így már van is visszacsatolásunk. Valóban nem az autójavítás problémája és szükséges ismeretanyaga ez, de ne adjuk alább, mert ma ez is az autó. Az autótechnika pedig a mi világunk.

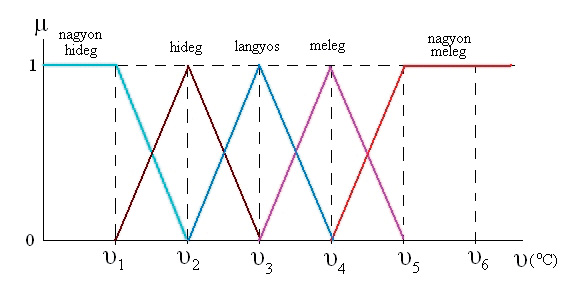
1. ábra

A fuzzy logika, logikai leírás egyik célja, hogy olyan módszerekkel szolgáljon, amelyekkel olyan problémák oldhatóak meg – méghozzá egyszerűen – amelyek túlságosan bonyolultak, vagy nehezen megfogalmazhatóak a hagyományos vizsgálati módszerekkel. A fuzzy jelentése: homályos, elmosódott, zavaros, kócos, bizonytalan, életlen vonalú, bizonytalan körvonalú stb. A fuzzy logika alkalmazásáról először a Berkeley-egyetem professzora, Latfi A. Zadek írt 1965-ben megjelent egyik tanulmányában, majd kidolgozta a „nyelvi változók” fogalmát, és azt egy 1973-as tanulmányában be is mutatta. Bebizonyította, hogy a fizikai jelenségek lineáris megközelítésével nem mindig lehet valós jelenséget pontosan leírni.

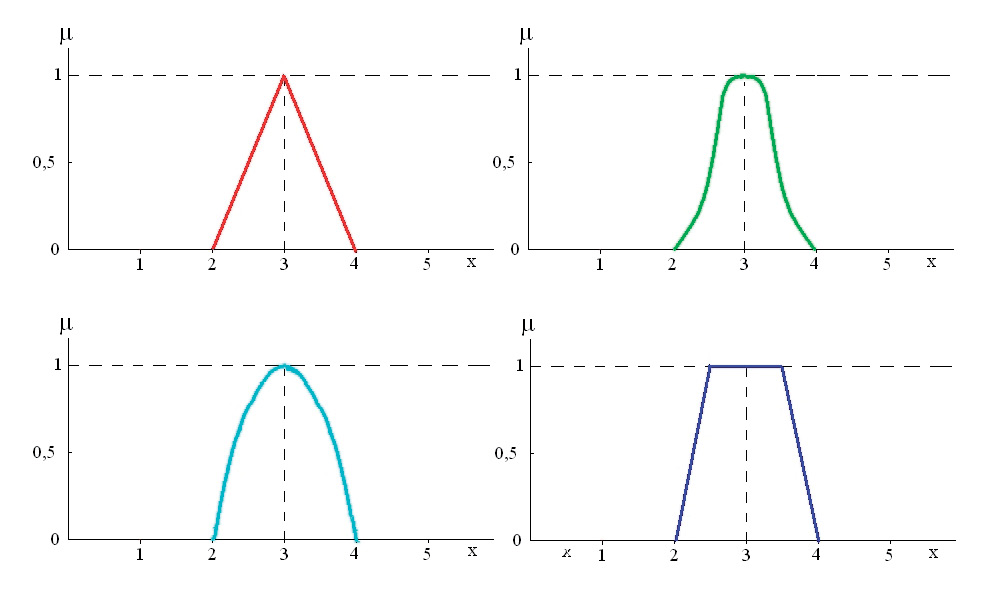
2. ábra

A fuzzy rendszereket az Egyesült Államokban hosszú ideig figyelmen kívül hagyták, mert a módszert alkalmatlannak tartották gyakorlati feladatok megoldására!

Nem úgy Japánban. Először a Hitachi emberei figyelmét keltette fel, akik azután a sendai vasúton egy igen jól működő szimulációt mutattak be. Ennek hatására alkalmazták ugyanitt a fuzzy rendszert gyorsítás, fékezés és megállás manőverei során már 1987-ben. Ezután a japán vállalatok egy igen széles termékskálát állítottak elő, a mosógépektől a fényképezőgépeken keresztül a légkondicionáló berendezésig. Több japán autógyártó vállalatnál megjelent a fuzzy logikán alapuló automatikus sebességváltóval rendelkező gépkocsi.

Bevezetés a fuzzy logikába

A logika formailag Arisztotelész tanításain alapul, ahol egy elem vagy tagja, vagy nem tagja egy halmaznak. Ha igen, akkor 1 (egy), ha nem akkor 0 (nulla) értéket vesz fel a logikai változó. Az arisztotelészi logikát a XIX. században G. Boole (1815–1864) foglalta rendszerbe. Más néven ezt a logikát kétértékű logikának is nevezzük. Autós példával az autó a parkolóban van vagy nincs a parkolóban, vagy az autó áll vagy megy stb. Viszont, mint később látni fogjuk, nem elégíti ki a kétértékű logika feltételeit az a példa, hogy a gépkocsi gyorsan megy vagy lassan megy, vagy melege van, illetve nincs melege. Ez azt jelenti, hogy minden fizikai jelenség nem alkalmas a Boole-féle logikával történő leírásra. A fuzzy logika jóval általánosabb adathalmazt tartalmaz a 0 és 1 között. Innen a neve „elmosódott, elkent halmazok logikája”. A korábbi példákból láthattuk, hogy a változók nem 0 és 1 logikai értékekből, sőt nem is egyéb számokból állnak, hanem „melléknevekből”. Ez teszi alkalmassá a fuzzy logikát arra, hogy olyan feladatokat oldhassunk meg vele, amelyek matematikailag egzakt módon nem írhatók le, ugyanakkor a hétköznapi nyelven történő megfogalmazása rendelkezésre áll. A nyelvi leírások jóval egyszerűbbek az ilyen problémák megoldására.

A fuzzy logika alkalmazásának vannak hátrányai is. Pl.: a fuzzy modell csak közelítő lehet, ezért ha pontos megoldásokra van szükség, akkor ott lehetőleg más megoldást kell keresni.

A következőkben a fuzzy logikához fűződő néhány alapfogalmat ismertetünk. Ezt a korábbi számainkban már érintettük, de célszerűségi okok miatt kibővítve ismét tárgyaljuk, mert elősegíti a jobb megértést.

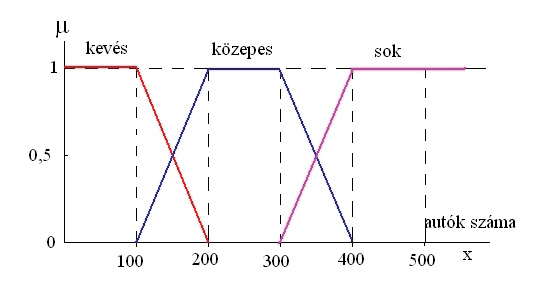
3. ábra

Néhány alapfogalom

1. Halmazok: tetszőleges dolgok összességét halmazoknak nevezzük. Az összességbe tartozó dolgok a halmaz elemei.

2. Crips: a fuzzy halmaztól való megkülönböztetés miatt a hagyományos (nem fuzzy) halmazokra elterjedt fogalom a crips (éles, határozott körvonalú) halmaz.

3. Tagsági függvény: minél kisebb vagy nagyobb mértékben tagja egy elem adott halmaznak, annál kisebb vagy nagyobb az elemre vonatkozó függvényérték. Ezt a függvényt nevezzük tagsági függvénynek, vagyis egy halmazhoz tartozó érték mértékét jelenti.

A tagsági függvényt lehet definiálni pl. a következő módon (1. sz. ábra). A lehetséges alakokat a 2. sz. ábra mutatja.

Autóspéldával élve a tagsági függvény értelmezésére írható:

HA (fékhőmérséklet = meleg) ÉS (sebesség = NEM nagyon gyors)

AKKOR (féknyomás = kissé csökkentve).

Ennél a példánál a két bemeneti változó a fékhőmérséklet és sebesség, a kimeneti változó pedig a féknyomás.

A féknyomás pl. a következő értékeket veheti fel:

– kissé csökkentve,

– csökkentve,

– változatlan,

– kissé növelve,

– növelve.

4. Tagsági függvény értékkészlete

A tagsági függvény értékkészletének a 0…1 intervallumot tekintjük és �-vel jelöljük.

5. Fuzzy halmaz: a tagsági függvény által definiált halmazt nevezzük fuzzy halmaznak. A fuzzy halmazok alkalmasak a bizonytalan határokkal rendelkező természetes nyelvi fogalmak reprezentálására.

Álljon itt példaként pl. a „kb. 3” fogalom értelmezése, amelyhez különböző alakú halmazok tartoznak (2. ábra). Az ábra szerinti halmazok jellemzői a következők: vegyük először a 2. a ábrát.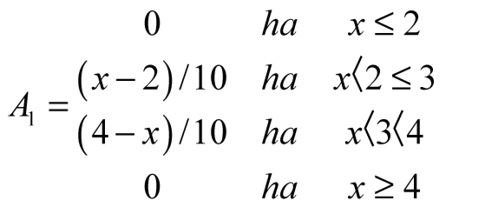

és

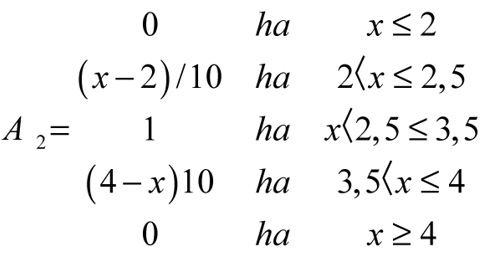
Vannak még egyéb halmazok (2. b és 2. c ábrák), de azokkal itt nem foglalkozunk.

6. Nyelvi változó: a nyelvi vagy lingvinisztikai változó elnevezést Zadeh vezette be. Értékei természetes nyelvi szavak lehetnek, pl.: nagyon rövid, rövid, átlagos hosszúságú, hosszú, nagyon hosszú. Egy másik példa, nagyon gyors, gyors, átlagos sebességű, lassú, nagyon lassú és még számtalan példát sorolhatnánk.

A nyelvi változókat fuzzy halmazokkal adjuk meg.

7. Fuzzyfikáció (fuzzyfikálás): a bemeneti változók (halmazok) fuzzy halmazzá történő átalakítása, vagyis a valós értékek lefordítása nyelvi kifejezésekre.

Mint tudjuk a nyelvi változók értékei szavak, mondatok lehetnek. A legtöbb valós helyzetben egy precíz válasz nem feltétlenül az optimális megoldást jelenti a problémára. A fuzzy logika kiterjeszti a szigorú igaz/hamis osztályozást olyan fogalmakkal, mint pl.: általában igaz, nagyjából igaz, igaz, valószínűleg rossz, rossz, teljesen rossz stb.

Pl.: végezzünk el egy fuzzyfikálást az úttesten lévő autók száma alapján három nyelvi értékre; kevés, közepes és sok (3. ábra). Vagyis a valós érték a gépkocsik száma, míg a nyelvi érték a kevés, közepes és sok szavakat jelenti.

8. Fuzzy következtetés: a nyelvi változók közötti összefüggéseket definiáló szabályhalmaz kiértékelése. Pl.:

HA a sebesség nagy, AKKOR a fékerő nő.

Ez csak a szavak kombinációját jelenti, de nem ad számszerű értékelést arra, hogy mekkorával nőjön a fékerő. A fuzzy következtetés, tehát egyszerű nyelvi szabályokból áll pl.: ha M=N, akkor A=B, tehát a mindennapi közönséges nyelvet kell használni. 9. Defuzzyfikálás (defuzzyfikció): A 7. pontban definiált következtetés eredményét fordítja vissza a nyelvi kifejezésekről a valós értékre. Pl. az előbbi példával élve, a fékerő nő 100 kN értékre, vagy 10 kN értékkel nő. A választás csak a tervezőn múlik.

A leggyakrabban alkalmazott defuzzyfikációs módszerek:

a) Súlypont módszer (COG-Center of Gravity)

A leggyakrabban alkalmazott módszer. Nagyon egyszerűen alkalmazható háromszög vagy trapéz alakú szabályok esetében. A defuzzyfikált érték a halmaz súlypontja.

b) Maximumok közepe módszer (MOM-Mean of Maxima)

A defuzzyfikált érték a halmaz középértéke. Előnye, hogy szintén egyszerűen alkalmazható.

c) Középső maximum módszer (COM-
Center of Maxima)

A legnagyobb tagsági függvény értékű elemeiből választja ki a középsőt.

Nagyon hasonlít a súlyponti módszerhez, de annál bonyolultabb számítást képvisel.

10. Változók: értelmezését legegyszerűbben példákon keresztül mutatjuk be:

bemeneti változó: sebesség, kimeneti változó: fékerő

bemeneti változó: sebesség és kanyar ívsugara, kimeneti változó: fékerő,

bemeneti változó: hőmérséklet, kimeneti változó: keréknyomás.

11. Fuzzy alapműveletek

a) Fuzzy logikai ÉS

Legyen két osztály tagsága μα és μβ,akkor az ÉS megkapható mint a két tagsági érték minimuma: