...egy kis geometria

A TŐLEM MEGSZOKOTT BITEK ÉS AMPEREK HELYETT...

Nemrégiben volt egy vitám azzal kapcsolatban, hogy ha egy motoron felső holtpontba kell állítani a főtengelyt, akkor az indikátorórás módszer a pontosabb vagy az, amikor egy becsavart célszerszámra fektetjük föl a főtengely sonkáját. Azt gondolom nem kell kihangsúlyozni, hogy a technikában az a szó, hogy pontosan, nem értelmezhető. Helyette a mennyire pontatlanul kifejezés sokkal szemléletesebb, vagyis amikor megadjuk valaminek a névleges értékét, meg azt, hogy mennyire lehet tőle eltérni.

A vita egyáltalán nem elméleti síkon zajlott, van ugyanis egy 1,4 literes, közvetlen befecskendezésű, Seat márkájú benzines oktatómotorunk, amelynek a technológiája – némileg megtévesztő módon – mindkét megoldást tartalmazza.

Amennyiben ezen a motoron vezérműláncot szeretnénk cserélni, akkor a lánckerekeket teljesen fel kell lazítanunk, ékpálya pedig nincs. A motor működése tehát egyértelműen a beállítás pontosságától függ.

Létezik egy gyári célszerszámkészlet, illetve annak a Klann cég által gyártott megfelelője indikátoróra-tartóval és pozicionálóstifttel. A kereskedelemben kapható egyéb márkák ugyanakkor csak az óratartót adják, a stiftet nem...

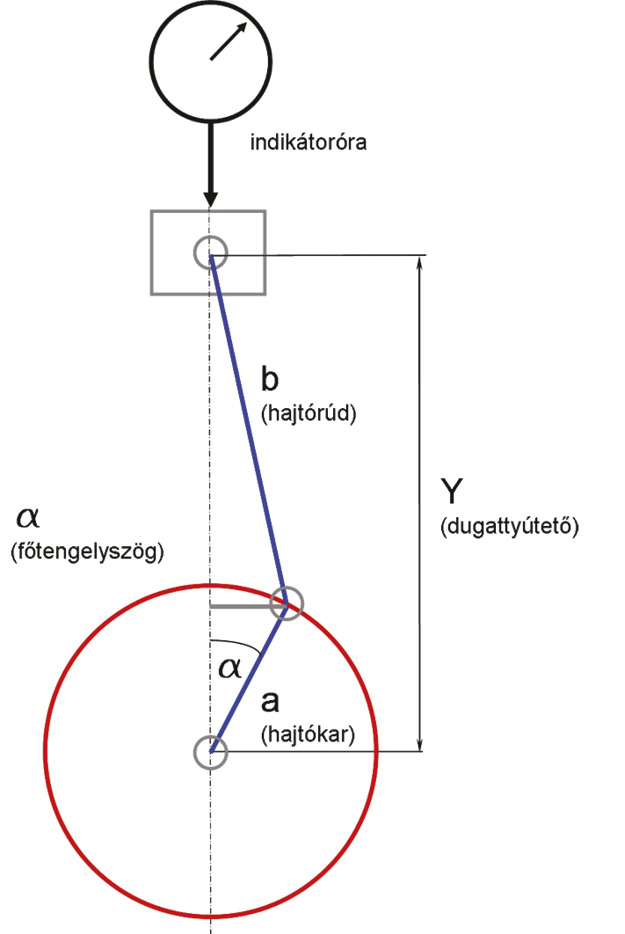
Az ábrákon jól látható, hogy a készüléket az 1. hengerbe kell becsavarni a gyertya helyére.

Ennél a motornál a gyertya pontosan centrálisan fekszik, így a mérés során az óra valóban a dugattyú szimmetriatengelyében mozdul el. A motor körbeforgatásával megkereshető az óra visszatérési pontja a felső holtpont (FHP) környékén, tehát meghatározható a felső holtpont.

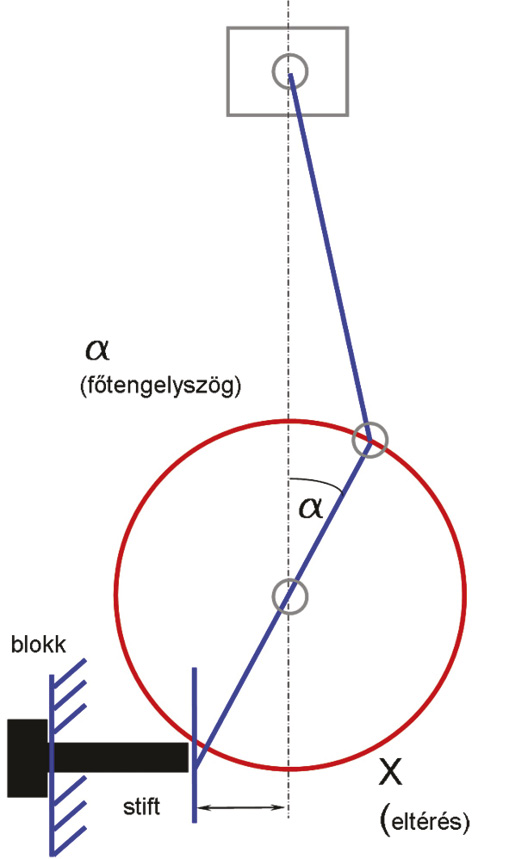
A másik megoldás esetén a főtengely egyik sonkáján van megmunkálva egy kis sík felület, ez a felület ütközik fel a blokk oldalába becsavart célszerszám homlokfelületén, amikor a főtengelyt forgásirányában forgatjuk.

Ez utóbbi módszer nagy előnye természetesen, hogy a főtengelycsavar meghúzása során a célszerszám ellentart – a kérdés tehát tulajdonképpen már valóban csak elméleti – ellentartás nélkül ugyanis a csavart nem szabad meghúzni. A gyakorlatban persze…

Amikor az indikátorórával mérünk, akkor az esetleges mérési hiba következtében a dugattyú teteje kicsit lejjebb vagy feljebb lesz, ennek következtében pedig a főtengely előrébb vagy hátrébb fordul. A magasságkülönbség a mellékelt ábra alapján (némi geometriai ismeret birtokában) felírható a forgattyúkar szögállásának függvényében – a képletből pedig meghatározható az adott mérési hibához tartozó szögeltérés.

A konkrét autó adatai:

hajtórúd: 138 mm

löket: 75,6 mm – ebből a forgattyúkar: 75,6/2=37,8 mm

tehát: a = 37,8 mm, b = 138 mm

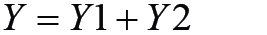
ahol

Y1 a forgattyúkar hengertengelyre vett vetületének a hossza.

Y2 a hajtórúd hengertengelyre vett vetületének a hossza,

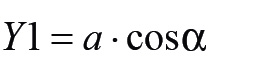
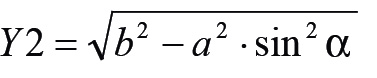
(egy kis Pithagorasz-tétel)

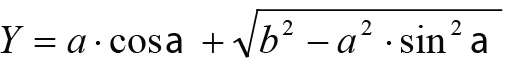
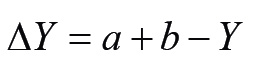
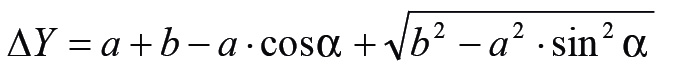
Ha feltételezzük, hogy 0,01 mm felbontású indikátorórát használva a mérés pontossága is 0,01 mm (ami egyébként nem igaz), akkor az ehhez a szélsőértékhez tartozó szöget kellene meghatároznunk. Nos, az α szögnek a végeredményként kapott egyenletből való kiszámítását inkább meghagynám a matematikusoknak. Lássunk egy lényegesen egyszerűbb megközelítést.

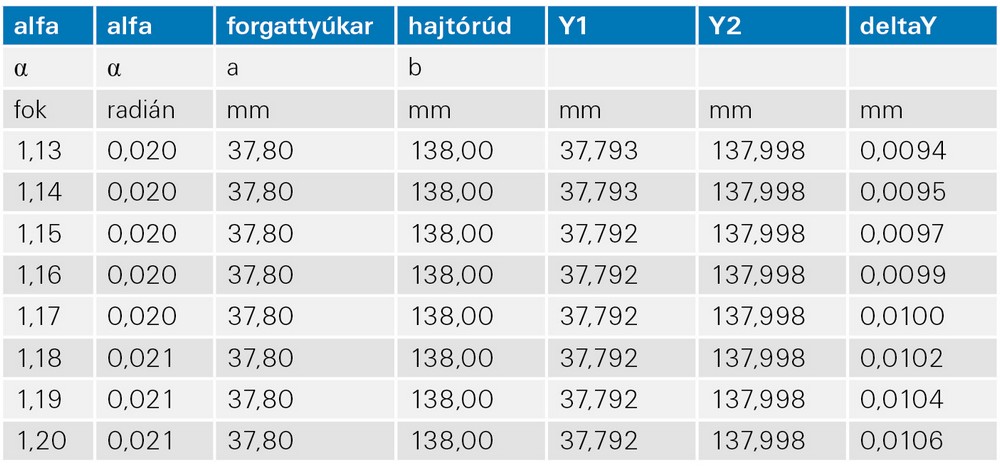
Ha az Excel táblázat soraiba beírjuk a ΔY képletét, majd a szöget elkezdjük tized-(század-)fokonként növelni, akkor valamelyik sorban megkapjuk a hozzávetőleg 0,01 mm-es értéket – és akkor már csak meg kell néznünk, melyik szögértékre kaptuk ezt (Mellékelten a táblázat kivonata).

Nos, az eredmény 1, 17 fokos szöghiba. Egy korszerű motor esetében ez véleményem szerint elfogadhatatlan, arról nem is beszélve, hogy mi csak a mérőóra felbontását vettük figyelembe, a pontossága ennél rosszabb, és az alkatrészek holtjátékáról sem beszélünk).

A másik esetben, amikor a pozicionálóstiftet használjuk, a hiba a stift tengelye irányába eső elmozdulás, ami ugyanannak a szögnek a szinuszával számítható, ekkor tehát a szöghiba értéke:

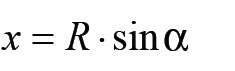
Ebből viszonylag könnyen kiszámítható, hogy:

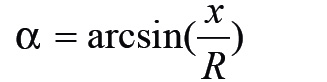
Motorunkon a felfektetési felület közepe az R = 40 mm sugarú körön található. Ennek alapján a csapos módszernél még a 0,1 mm-es (tehát tartható pontosságú) eltérés csak 0,14 fokos különbséget ad.

És akkor arról még nem is beszéltünk, hogy mi történik a csavar meghúzása során, amikor az alkatrészek a nagy nyomaték miatt elfordulnak egymáshoz képest..

Utóirat

Utólag persze kiderült, hogy arra a bizonyos szögre létezik egy közvetlen képlet, a koszinusztétel, amit gyakorlatilag szinte végig levezettem (matematikatanárom remélhetőleg nem olvassa az Autótechnikát).

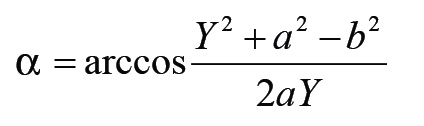
Ennek alapján, az ismert adatokkal, ha a mérési hiba 0,01 mm, akkor a szöghiba 1,168 fok.

Vagyis akik alaposan ismerik a geometriát, azoknak elég egyetlen képletet alkalmazni, akik nem, azoknak ott az Excel.

A célszerszámot azonban így is, úgy is meg kell vásárolniuk.